Introduction
二重降下現象(Double Descent)とは、統計学や機械学習において、モデルのパラメータ数を増やしていくにつれて一度は複雑性誤差が増加するが、その後再び誤差が減少していくという現象です。古典的な統計モデルでは、複雑性誤差が一度増加する手前でバイアスとバリアンスのトレードオフをとるようにモデルを調整することが一般的でしたが、現在の深層学習に代表されるような過剰パラメータモデルでは、パラメータを増やせば増やすほど誤差を減らすことができる場合があるということで、ある種現在の大規模なモデルが良いということの証左になっているともいえるでしょう(Neural Scaling Lawとかの方が説得力は強いと思いますが)。
今回はこのDouble Descentを実験で確かめてみます。下の論文をもとに実装してみました。
実験設定
データ
入力 $d$ 次元、出力 $1$次元のデータが $n$ 個与えられるとします: ${(\boldsymbol{x} _ i,y _ i)} _ {i=1} ^ n\subset\mathbb{R}^d\times \mathbb{R}$
制約条件: $\boldsymbol{x} _ i\overset{\mathrm{i.i.d.}}{\sim} \mathrm{Unif}(\mathbb{S} ^ {d-1}(\sqrt{d}))$ かつ $f _ d \in L ^ 2(\mathbb{S} ^ {d-1}(\sqrt{d}))$ を使って以下の形で書けているとします: $$y _ i=f _ d(\boldsymbol{x} _ i)+\varepsilon _ i, \quad \varepsilon _ i \overset{\mathrm{i.i.d.}}{\sim} \mathcal { N }(0, τ ^ 2 ) $$
ここで $\mathrm{Unif}(\mathbb{S} ^ {d-1}(r))$ は半径 $r$ の $d$ 次元球面上での一様分布を表す: $\boldsymbol{x}\sim \mathrm{Unif}(\mathbb{S} ^ {d-1}(r))$ は $\lVert\boldsymbol{x}\rVert _ 2=r$ になっています。
特に今回は $\boldsymbol{w}\sim\mathrm{Unif}(\mathbb{S} ^ {n-1}(1))$ をとって固定して $f_d(\boldsymbol{x}) = \boldsymbol{w} ^ \top \boldsymbol{x}$ で定め、単純な線形関係にノイズが乗ったものとします:
$$ y _ i = \boldsymbol{w} ^ \top \boldsymbol{x} _ {i} +\varepsilon _ i,\quad \varepsilon _ i \overset{\mathrm{i.i.d.}}{\sim} \mathcal { N }(0, τ ^ 2 ) $$
モデル
Random Feature Regressionを行います。まずは $i=1,\ldots, N$ に対して以下の関数を考えます。
$$ f(\boldsymbol{x};\boldsymbol{a},\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N)=\sum _ {i=1} ^ Na _ iσ\left(\frac{\boldsymbol{\theta} _ i ^ \top \boldsymbol{x}}{\sqrt{d}}\right),\quad σ(x)=\mathrm{ReLU}(x)=\max\lbrace 0,x \rbrace $$
ここで $\boldsymbol{\theta} _ i\overset{\mathrm{i.i.d.}}{\sim}\mathrm{Unif}(\mathbb{S} ^ {d-1}(\sqrt{d}))$ をとって固定することにし、$\boldsymbol{a}=(a _ 1,\ldots, a _ N) ^ \top\in\mathbb{R} ^ N$ はRidge回帰によって決めます:
$$ \hat{\boldsymbol{a}}(\lambda)=\arg\min _ {\boldsymbol{a}\in\mathbb{R} ^ N}\left \lbrace \frac{1}{n}\sum _ {j=1} ^ n\left(y _ j-f(\boldsymbol{x} _ j;\boldsymbol{a},\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N)\right) ^ 2+\frac{N\lambda}{d}\lVert\boldsymbol{a}\rVert ^ 2 _ 2\right \rbrace $$
これは、$ \boldsymbol{X} = \left(σ\left(\frac{\boldsymbol{\theta} _ j ^ \top \boldsymbol{x} _ i}{\sqrt{d}}\right)\right)_{ij} \in \mathbb{R} ^{n\times N}$ とおくと
$$ \hat{\boldsymbol{a}}(\lambda) = \left( \boldsymbol{X} ^ \top \boldsymbol{X} + \frac{N\lambda}{d} \boldsymbol{I} _ {n\times n}\right) ^ + \boldsymbol{X} ^\top \boldsymbol{y} $$
となります。ここで$^ +$ は擬似逆行列を表しています。数値安定性みたいなのを気にしなければ普通に逆行列でいいと思います。その方が計算早いし。
このときの $f$ は、2層のニューラルネットワークの特殊な形で、1層目の重みが固定されているおかげで( $d$ 次元の入力データが $N$ 次元のRandom Featureに飛ばされます)2層目を線形回帰(今回はRidge回帰)と同様に求めることができます(cf. カーネル法)。
誤差の評価
次のような二乗和誤差を使います:
$$ R(f _ d,\boldsymbol{x} _ 1,\ldots,\boldsymbol{x} _ n,\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N,\lambda) = E _ {\boldsymbol{x}}[\left(f _ d(\boldsymbol{x})-f(\boldsymbol{x};\hat{\boldsymbol{a}}(\lambda),\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N)\right) ^ 2] $$
経験分布に対しては
$$ \hat{R}(f _ d,\boldsymbol{x} _ 1,\ldots,\boldsymbol{x} _ n,\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N,\lambda) = \frac{1}{n}\sum _ {j=1} ^ n\left(f _ d(\boldsymbol{x} _ j)-f(\boldsymbol{x} _ j;\hat{\boldsymbol{a}}(\lambda),\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N)\right) ^ 2 $$
で $R$ を推定します。
漸近挙動
非常に複雑ですが、 $\lambda\to 0, d\to\infty$ の場合の漸近的な挙動の解析解が知られています。
現在の設定において
$$ f _ d(\boldsymbol{x})=\boldsymbol{w} ^ \top\boldsymbol{x} $$
であり、$\lVert\boldsymbol{w}\rVert _ 2 ^ 2=F _ 1 ^ 2 (=1)$ でした(論文中では $F _ 1 ^ 2$ と表記されている)。また $τ ^ 2$ は、観測データに入り込むノイズの分散、すなわち、観測データが $(\boldsymbol{x},y)$ だったとき
$$ y = f _ d(\boldsymbol{x}) +\varepsilon,\quad\varepsilon \sim\mathcal{N}(0,τ ^ 2) $$
だったことを思い出します(数値実験では $τ ^ 2= 1/5$ としています)。
$G\sim\mathcal{N}(0,1)$ と $σ(x)=\mathrm{ReLU}(x)=\max \lbrace 0,x \rbrace $ として
$$ \begin{split} \mu _ 0 & = E[σ(G)] = E[\max \lbrace 0,G \rbrace ]=\frac{1}{\sqrt{2\pi}} \cr \mu _ 1 & = E[Gσ(G)] = E[\max \lbrace 0,G ^ 2 \rbrace ]=\frac{1}{2}\cr \mu _ \star ^ 2 &= E[σ(G) ^ 2]-\mu _ 0 ^ 2-\mu _ 1 ^ 2=E[\max \lbrace 0,G ^ 2 \rbrace ]-\mu _ 0 ^ 2-\mu _ 1 ^ 2=\frac{1}{4}-\frac{1}{2\pi} \end{split} $$
これより
$$ \zeta=\frac{\mu _ 1}{\mu _ \star}=\frac{1}{\sqrt{\frac{1}{2}-\frac{1}{\pi}}} $$
を定めます。次に $\psi = \min \lbrace \psi _ 1, \psi _ 2 \rbrace $ として
$$ \chi = -\frac{\left[ \left( \psi\zeta ^ 2 - \zeta ^ 2 - 1) ^ 2 \right) ^ 2 + 4\zeta ^ 2\psi \right] ^ {1/2} + \left( \psi\zeta ^ 2 - \zeta ^ 2 - 1 \right) }{ 2\zeta ^ 2} $$
を定めます。これを使って
$$ \begin{split} \mathscr{E} _ {0,\text{rless}}(\zeta, \psi _ 1, \psi _ 2) &= - \chi ^ 5 \zeta ^ 6 + 3\chi ^ 4 \zeta ^ 4 + (\psi _ 1 \psi _ 2 - \psi _ 2 - \psi _ 1 + 1)\chi ^ 3 \zeta ^ 6 - 2\chi ^ 3 \zeta ^ 4 - 3\chi ^ 3 \zeta ^ 2 \cr &\quad + (\psi _ 1 + \psi _ 2 - 3 \psi _ 1 \psi _ 2 + 1)\chi ^ 2 \zeta ^ 4 + 2\chi ^ 2\zeta ^ 2 + 2\chi ^ 2 + 3 \psi _ 1 \psi _ 2 \chi \zeta ^ 2 - \psi _ 1 \psi _ 2, \notag \cr \mathscr{E} _ {1,\text{rless}}(\zeta, \psi _ 1, \psi _ 2) &= \psi _ 2 \chi ^ 3 \zeta ^ 4 - \psi _ 2 \chi ^ 2 \zeta ^ 2 + \psi _ 1 \psi _ 2 \chi \zeta ^ 2 - \psi _ 1 \psi _ 2, \cr \mathscr{E} _ {2,\text{rless}}(\zeta, \psi _ 1, \psi _ 2) &= \chi ^ 5 \zeta ^ 6 - 3\chi ^ 4 \zeta ^ 4 + (\psi _ 1 - 1)\chi ^ 3 \zeta ^ 6 + 2\chi ^ 3 \zeta ^ 4 + 3\chi ^ 3 \zeta ^ 2 + (-\psi _ 1 -1)\chi ^ 2 \zeta ^ 4 - 2\chi ^ 2 \zeta ^ 2 - \chi ^ 2, \notag \end{split} $$
から
$$ \begin{split} \mathscr{B} _ {\text{rless}}(\zeta, \psi _ 1, \psi _ 2) &= \frac{\mathscr{E} _ {1,\text{rless}}}{\mathcal{E} _ {0,\text{rless}}},\cr \mathscr{V} _ {\text{rless}}(\zeta, \psi _ 1, \psi _ 2) &= \frac{\mathscr{E} _ {2,\text{rless}}}{\mathscr{E} _ {0,\text{rless}}} \end{split} $$
で記号を定めると
$$ \lim _ {\lambda\to 0}\lim _ {d\to 0}E[R(f _ d,\boldsymbol{x} _ 1,\ldots,\boldsymbol{x} _ n,\boldsymbol{\theta} _ 1,\ldots,\boldsymbol{\theta} _ N,\lambda)]=F _ 1 ^ 2\mathscr{B} _ {\text{rless}}(\zeta, \psi _ 1, \psi _ 2)+τ ^ 2\mathscr{V} _ {\text{rless}}(\zeta, \psi _ 1, \psi _ 2) $$
となることが導けるそうです。
実装
実験結果
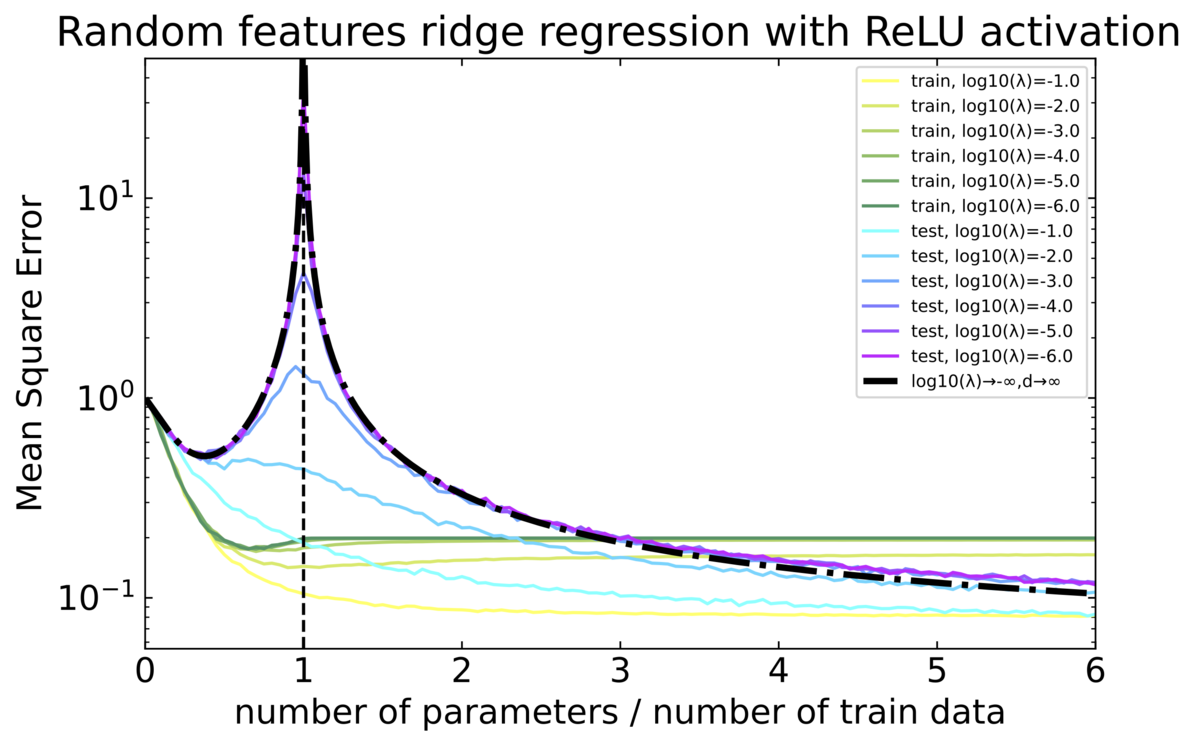
パラメータは $d=100,n=500,N=25,50,\ldots,3000$ として、横軸は $N/n$ で縦軸は $\hat{R}$ としています。青色のテストデータに対する誤差に注目すると、 $N/n=1$ では $\lambda\to 0$ で発散する様子が見受けられ、また二重降下している様子も良く見えます。なお、黒線は上で示した解析解をプロットしています。